Year 7
Algebraic Thinking: Equality and Equivalence, Algebraic Notation, Sequences

Sequences and pattern spotting are at the very heart of mathematical thinking. The ability to spot a pattern both in diagrams and numbers enables one to spot trends and make predictions on outcomes. Students will also begin to learn how to use algebra to generalise the structure of arithmetic, including to formulate mathematical relationships.
Read MorePlace Value and Proportion: FDP equivalence, Place Value and Ordering Numbers
In this unit students will explore integers up to one billion and decimals to hundredths. Students will gain a deeper understanding of the links between fractions, decimals and percentages so that they can convert fluently between those most commonly seen in real life.
Read MoreApplications of number: Solving Problems with Multiplication/Division, Solving Problems with Addition/Subtraction
Number is at the heart of our Year 7 curriculum as this enables students to be successful in all other strands of mathematics. Calculator use is discouraged in this unit to promote further fluency with written methods.
Read MoreDirected Number and Fractional Thinking: Addition and Subtraction of Fractions, Operations and Equations with Directed Numbers
This unit is designed to extend and deepen pupils understanding of directed numbers and fractions. Students will use a vertical number line alongside double sided counters to represent and work with directed numbers. Students will use a horizontal number line alongside multiple representations to develop students conceptual understanding of fractions. These representations and contexts will be used to ensure pupils appreciate the meaning these types of numbers rather than relying on a set of potentially confusing “rules”.
Read MoreLines and Angles: Developing Geometric Reasoning, Constructing, Measuring and Using Geometric Notation
Students will build on their KS2 skills using rulers and protractors to construct and measure increasingly complex diagrams using correct mathematical notation. This will include three letter notation for angles, the use of hatch marks to indicate equality and the use of arrows to indicate parallel lines. Pie charts will also be studied here to gain further practice measuring and drawing angles. Basic geometric language, names and properties of types of triangles, quadrilaterals and polygons will be introduced this half term. Angle relationships will be built on from knowledge and understanding from KS2 to include the use of parallel lines.
Read MorePrime Numbers and Proof, Sets and Probability
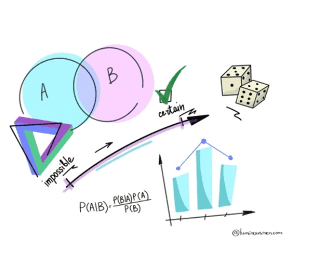
We use probability in our daily lives to help make decisions when we don't immediately know what the outcome will be to determine the best course of action. In this unit probabilty is introduced and linked to fractions and decimals. Venn diagrams are taught as a sorting structure for both probability and numerical problems.
Read MoreYear 8
Proportional Reasoning: Ratio and Scale
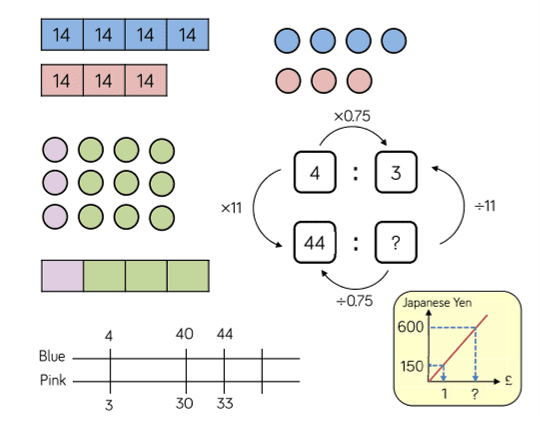
In the first half term of Year 8, students will explore the concept of ratio and use bar models, double number lines and ratio tables to develop deep and connected understanding of ratio and proportion.
The links between ratio and fractions are will also be explored with pi introduced as the ratio of the circumference of a circle to its diameter. Conversion graphs are used as a contextual introduction to direct proportion with later work with maps and scales.
Representations: Tables & Probability, Working in the cartesian plane
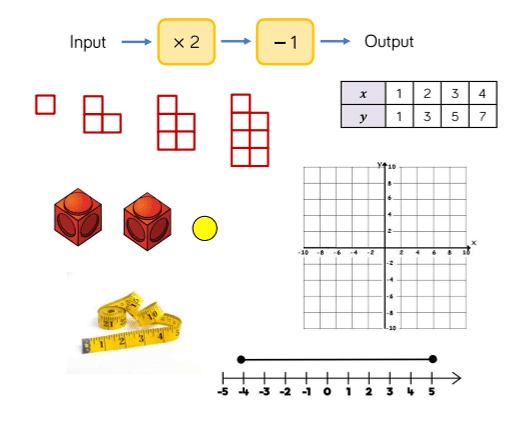
This half term students will be building on their knowledge of coordinates from KS2 by looking formally at algebraic rules for straight lines starting with lines parallel to the coordinate axes but developing understanding of straight lines in the form y = mx + c and links graphs to sequences.
Following this students are introduced to bivariate data and the concept of linear correlation. They will extend their knowledge from KS2 to work with both discrete and continuous data.
Building from Year 7 and earlier lessons on two way tables learners work with the idea of probability and how to calculate probabilities from two-way tables and Venn diagrams.
Algebraic Techniques: Indices, Sequences, Brackets, equations and inequalities

Students will learn how manipulate more complex algebraic expressions including how to expand brackets and factorise. All students will revisit and extend their knowledge of how to solve linear equations, now to include brackets and the unknown on both sides. Students will also understand how to solve formal inequalities for the first time, learning the meaning of a solution set.
Following this learners will look at sequences with more complex algebraic rules now that students are familiar with a wider range of notation.
Lastly learners will explore the ideas behind the addition and subtraction laws of indices which will be revisited when standard form is revisited when standard form is studied next term.
Developing Number: Multiplication and Division with fractions, Percentages

The relationships between fractions and percentages including decimal equivalents are explored this half term. Students will be using this equivalence to work out percentage increase and decrease both with and without a calculator.
Read MoreDeveloping Geometry: Symmetry and reflection, Area and Perimeter of Circles, Angles in polygons

Students will extend their knowledge and understanding of angle facts from Year 7 and solve increasingly complex angle problems. Links are then make to the connected properties of polygons and quadrilaterals. Students will also learn about further constructions with pairs of compasses.
Following this students will consolidate their understanding of how to find the area of trapezia from Year 7 and extend this to include circles and common sectors. A key aspect of this half term is for learners to be able to choose and use correct formulae reinforcing shapes the names of shapes and their properties.
Transforming shapes by reflection and understanding line symmetry and rotational symmetry is developed at the end of this half term. Here students will also revisit and enhance their knowledge of types of triangles and quadrilaterals.
Reasoning with Data: Measures of Location, The Data Handling Cycle

In this unit there is a particular focus on using charts to
compare different distributions. Students also explore when graphs may be
misleading, an important real-life consideration. Collection of data is also
covered, including designing and criticising questionnaires.This half term
reintroduces the mode and also looks at when and why each average should be
used. Students will also look at the mean from grouped
and ungrouped frequency tables. We also consider outliers, considering what effect
these have on all the measures studied, and whether they should be included or
excluded in our calculations.
Year 9
Coordinate Geometry: Speed, distance and time,Graphs and algebra

Students will learn how to manipulate algebraic formulae which will form the basis of their knowledge and understanding of formulae used throughout maths and science. They will develop understanding of straight line graphs and what each variable in the formula represents, including what changes when you have a parallel or perpendicular line. This will extend to plotting and solving graphically with more complex graphs such as quadratics.
Read MoreWorking in 2 and 3 Dimensions: Three-dimensional shapes

Students will be formally working with 3D shapes this half term; using language and properties of shapes to precisely describe and analysis cuboids, prisms, cylinders, pyramids, cones and spheres.
Following this students will use volume to solve problems with density and rates of flow.
Money Matter: Maths and Moneys

Students will developing their prior understanding of numerical and graphical concepts through a variety of financial contexts. Additional language of financial mathematics is introduced along with simple ideas of tax and wages. Percentages are further explored in various contexts including simple and compound interest.
Read MoreFurther angles and Transformations: Similar Shapes, Rotation and Translation, Angles and Bearings

During this half term students will revise and extend their knowledge of angles and properties of shapes applying them to increasingly complex problems including bearings.
Additionally students will be building on their prior learning of transformations from Year 7 & 8 to compare different effects of transformations on congruency. Similar shapes are also taught and this is linked to an introduction to Trigonometry.
Pythagoras Theorem and Surds

During this half term students will squares and square roots before moving on to investigate the relationship between the sides of a right-angled triangle. The converse of the theorem is emphasised so that students are aware that if the sides of a triangle satisfy the rule then the triangle must be right-angled. Students explore the theorem in context, including on coordinate axes and 3D shapes.
Additionally students will be introduced to the idea of irrational numbers and work with surds as this links to solutions often found when working with Pythagoras Theorem.
Probability & sample space diagrams: Venn Diagrams, Tree Diagrams, Probability

During this half term students will build on their learning in Year 7 and 8 to calculate the probabilities of single and combined events. A key focus is the introduction of independent events and the use of the multiplication rule. Students will also look at a variety of diagrams that support probability such as sample space diagrams, Venn diagrams and two-way tables. Tree diagrams are considered both with and without replacement.
Read MoreYear 10
SIMILARITY & TRIGONOMETRY: Trigonometry, Congruence, similarity & enlargement,

Trigonometry is introduced as a special case of similarity within right-angled
triangles linking to the introductory lesson in Year 9 and the concept of similarity. Emphasis is placed throughout the steps on linking the trigonmetric functions to ratios, rather than just functions.
This key topic is introduced early in Year 10 to allow regular revisiting and linkink to other concepts eg. bearings
Developing Algebra: Working with Quadratics,Simulataneous Equations

Students will be revisiting and then building on their understanding of how to form and solve linear equations from KS3 to find the solution of simultaneous equations by both algebraic and graphical methods.
Expanding brackets will be revisited as an introduction to factorising and solving quadratics. Higher tier students will then have the knowledge and understanding required to solve sets of simultaneous equations where one is linear and the other is quadratic following learning all methods of solving a quadratic equation.
Graphs and Circles, Working with circles

Circles are explored in depth in this unit. From area of sectors to arc length and angle properties, circles and their properties are taught this half term. This is then extended to allow students to work out volume and surface area of shapes including cones, spheres and hemi-spheres. Higher tier students also learn how a circle can be represented on the cartesian plane.
Read MoreFurther Probability & Combinatorics

In this unit students will be understanding how a tree diagram can structure a probaibility problem. Students will be both constructing, using and critiquing all types of sample space diagrams and deciding which representation is best for a given problem.
Read MoreDelving into data
This unit builds on the KS3 work of collection, representation and use of summary statistics to describe and analyse data. For students following higher tier there is additional content relating to continous data including Histograms, cumulative frequency, box plots and associated measures.
Read MoreSequences, Indices and Surds

Sequences are explored in this half term with higher tier students working with quadratic sequences and nth term. The link between indices and surds is highlighted and further rules of indices are introduced. Negative indices is also linked to standard form in this unit.
Read MoreYear 11
Further Geometry: Vector Geometry, Transforming Shapes
Students learn how to combine transformations to transform 2D shapes on a cartesian grid including considering how certain transformations create invariate points. This then leads on to revisiting vectors and extending this to learn about further vector geometry
Read MoreFurther Algebra: Functions, Changing the subject,Proof

Students will be using their algebraic manipulation skills to prove a variety of algebraic statements. Following this students will rearrange complex formulae to support their learning of functions.
Read MoreFurther Reasoning: Algebraic, Graphs, Bounds
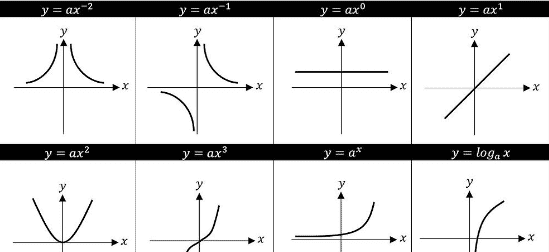
In this half term students will be considering error intervals and bounds of measurement problems. In addition to this students will be plotting non-linear functions and learning about the properties of each graph. This work with graphs is extended to include speed-time graphs and other piece-wise graphs.
Read More